
立方体の角を落した形。一見ばらばらの形のピースから、立方体におさまる立体が現われるところがミソです。
まず、立方体の角をどう落すかを決めます。
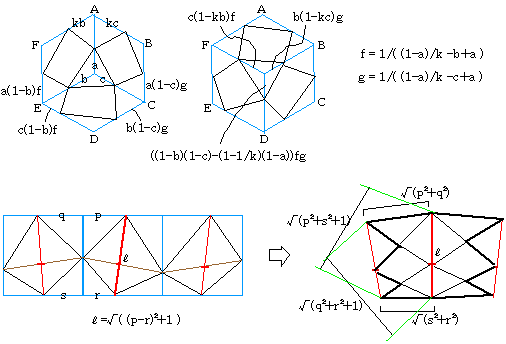
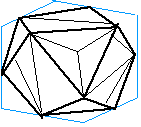
立方体の1辺の長さを1とします。くみがみの外形の四角形は、対面同士で対応する辺が各々平行でなければいけません。(さもないと、くみがみのピースがねじれてしまう) この条件から外形の四角形は全く任意とはいかず、1頂点の切片長さa,b,cと係数k(上図)で形が決まります。ピースの形は、この四角形の頂点間の距離から、上図のように求まります。
不規則な四角形の12面体。
正方形に内接する(合同でない)2つの四角形の対応する辺が各々平行になる、言い換えると各辺を平行移動しても正方形に内接したままでいられる条件は、数式では次のようにまとめられます。
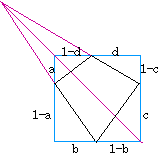
abcd=(1-a)(1-b)(1-c)(1-d)
これは、図では 内接四角形の1組の対辺とそれに挟まれた正方形の対角線の各延長線が1点で交わる(または平行)ということに相当します。(上図) この条件がみたされるとき、内接四角形の残りの対辺についても同じ条件がみたされます。このことは、デザルグの定理というのだそうです。また、以上のことは、外側が正方形でなくてもよく、任意の四角形についてあてはまります。